
Simple shear and moment diagrams how to#
The Postprocess module is used to plot the responses of the beam from the analysis, including force diagrams and deflections.įor an indepth understanding and how to customize the existing planeSections library classes and methods, check the documenation.The Diagram module is used to plot the beam model.The Analysis module is used to analyze the beam using OpenSeesPy and document the results.The beam class is the core class of the module, and the one the user interacts with the most. The Builder module is used to create the beam and beam elements.PlaneSection library has four core modules which are as follows: Being built on OpenSees, the structural results are reliable, and there is lots of room to create more complex models. Beginning the shear diagram at the left, V immediately jumps down to a value of q 0 L / 8 in opposition to the. Replacing the distributed load by a concentrated. The reactions at the supports are found from static equilibrium. The aim of PlaneSections is to make beam analyses easier, which can be used to document structural calculations quickly. 4.1: Shear and Bending Moment Diagrams 1. PlaneSections is a lightweight finite element beam bending library built on OpenSeesPy. Hence, for those of us with an interest in developing finite element tools for structural analysis, this instructable is about how to create a simple beam model and plot its shear force and bending moment diagram using a python library called planeSections created by csbloom which is built upon openseesPy This analysis and cross-checking are tedious and time-consuming when verifying our results by hand. In addition, when given a reinforced concrete design project, we also start by analyzing our beam elements, which transfer wall and slab load to columns and from column to foundation. This gets more complicated when doing beam analysis, as we are trying to get what our beam element's shear force and bending moment diagram will look like. Note: The negative sign indicates that the bending moment is acting in the opposite direction to the positive direction of the axis.For those of us taking structural mechanics and strength of materials courses, we all know how difficult it can get when trying to verify our analysis results. Therefore, the maximum bending moment is 12.5 kNm (acting downwards) at point C. At this point, the shear force is -5 kN (since it is acting downwards) and the moment is -12.5 kNm (since it is also acting downwards). The maximum bending moment occurs at the point of maximum shear force, which is at point C. Step 4: Determine the maximum bending moment Therefore, the moment diagram looks like this:
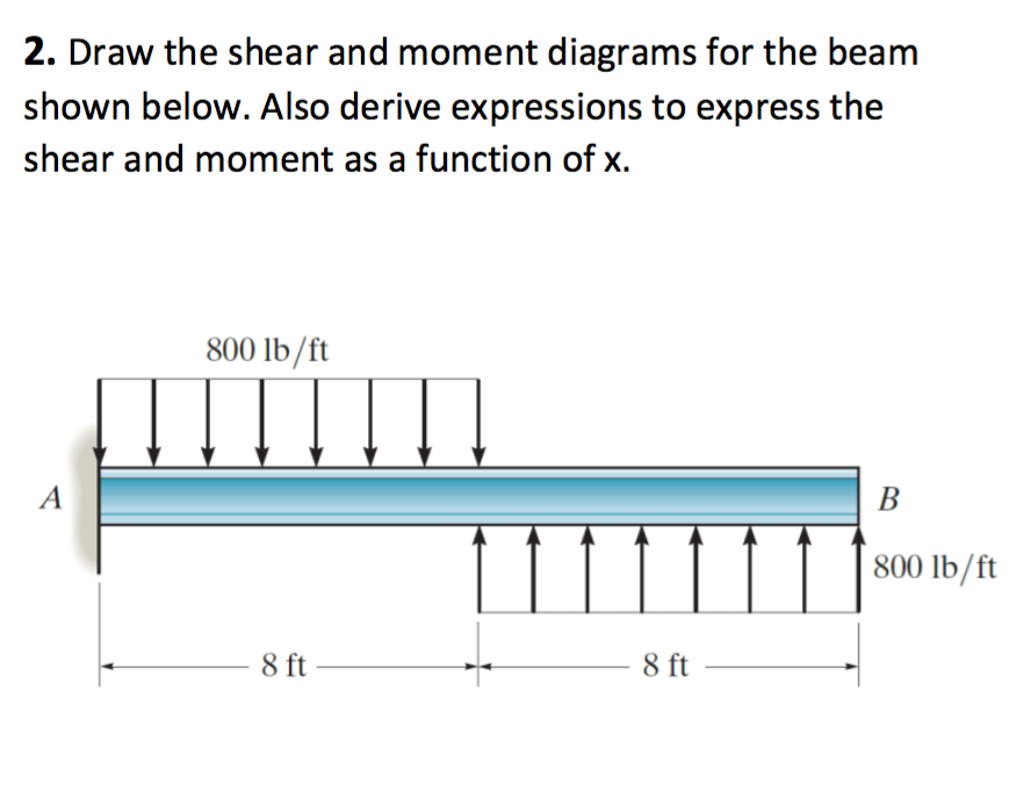
Finally, at point B, the moment drops by 2.5x (due to the reaction at B). This is in reference to property number 2, that when the shear (also the slope of the moment diagram) is zero, the tangent drawn to the moment diagram is horizontal. The maximum moment occurs at the point of zero shears.
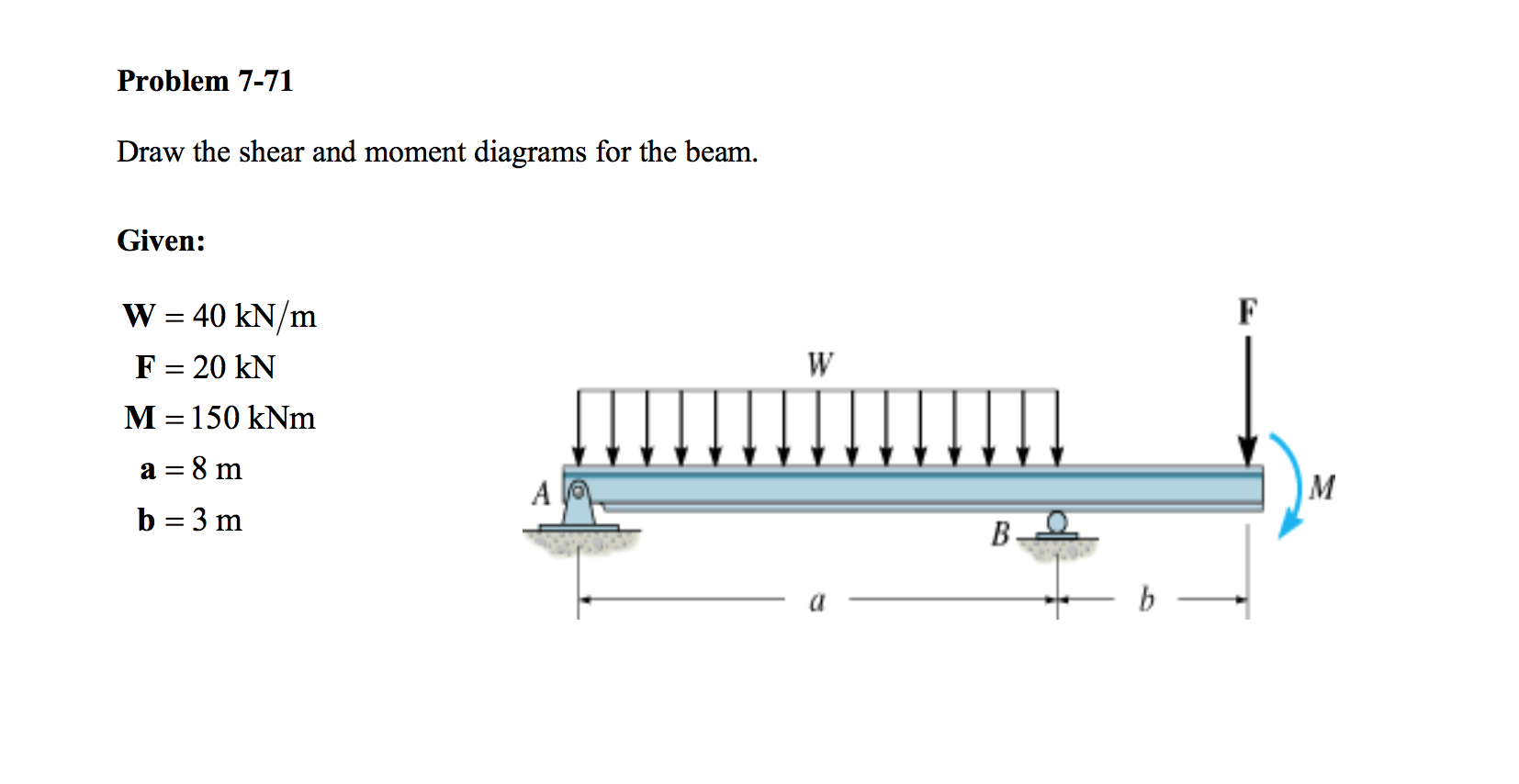
At point C, the moment suddenly drops by 5x (due to the point load). The slope of the shear diagram at a given point equals the load at that point. These diagrams provide valuable insights into how the shear force and bending moment vary along the length of the beam. As we move to the right, the moment increases by 2.5x (where x is the distance from A). Shear and moment diagrams are graphical representations of the internal forces and moments within a beam. We start at one end of the beam and work our way to the other end, keeping track of the changes in moment at each point.Īt point A, the moment is zero (since there is no load to the left of A). To draw the moment diagram, we need to integrate the shear diagram. Therefore, the shear diagram looks like this: Finally, at point B, the shear force drops by 2.5 kN (due to the reaction at B). At point C, the shear force suddenly drops by 5 kN (due to the point load). As we move to the right, the shear force increases by 2.5 kN (due to the reaction at A). To draw the shear diagram, we need to start at one end of the beam and work our way to the other end, keeping track of the changes in shear force at each point.Īt point A, the shear force is zero (since there is no load to the left of A). Reaction at support A = Reaction at support B = 5/2 = 2.5 kN Therefore, each reaction will be half of the total load on the beam, which is 5 kN. Since the beam is simply supported, the reactions at the supports will be equal and opposite.
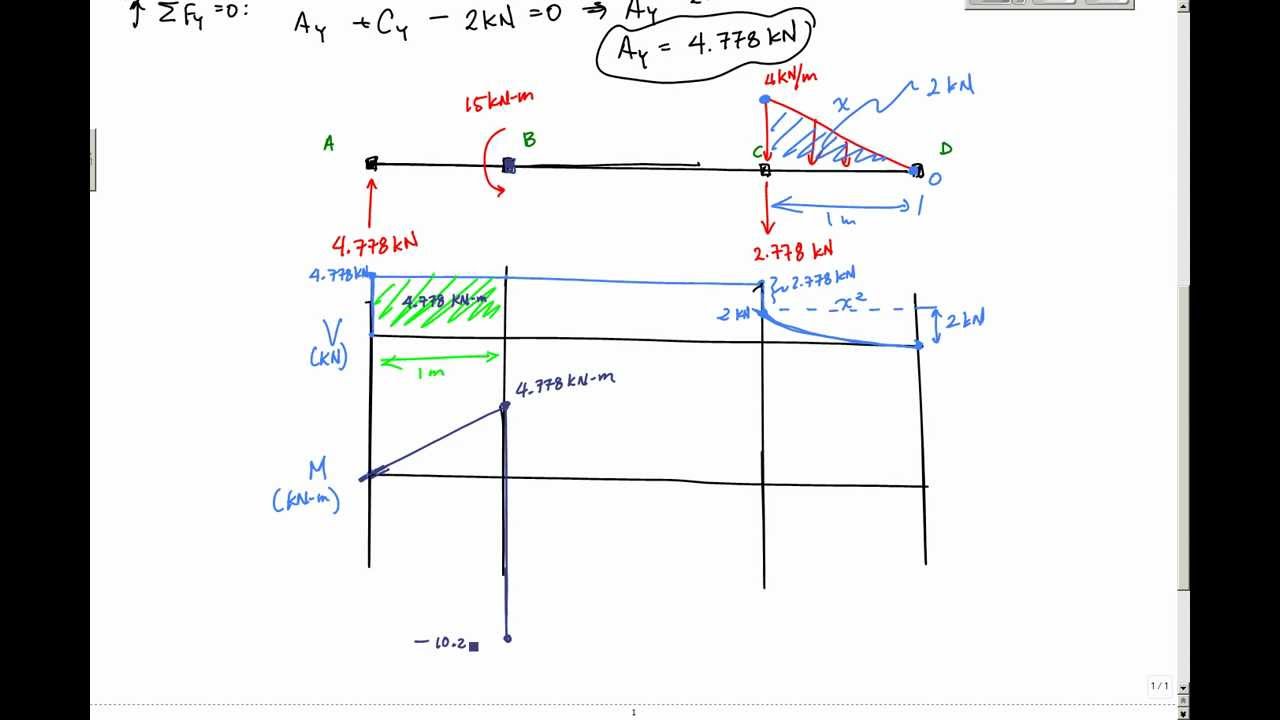

Step 1: Determine the reactions at the supports


 0 kommentar(er)
0 kommentar(er)
